Giải bài tập Vận dụng 2 trang 49 Toán lớp 10 Tập 2 | Toán 10 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng 2 trang 49 Toán lớp 10 Tập 2. Bài 2: Đường thẳng trong mặt phẳng toạ độ. Toán 10 - Chân trời sáng tạo
Đề bài:
Một người đang lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định được một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm M(x; y) từ vị trí A(1; 2) chuyển động thẳng đều với vectơ vận tốc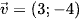 
.
a) Viết phương trình tổng quát của đường thẳng ∆ biểu diễn đường đi của điểm M.
b) Tìm tọa độ của điểm M khi ∆ cắt trục hoành.
Đáp án và cách giải chi tiết:
a) Vì điểm M chuyển động thẳng đều với vectơ vận tốc 
và đường đi của điểm M là đường thẳng ∆. Do đó 
là vectơ chỉ phương của đường thẳng ∆.
Suy ra vectơ pháp tuyến ∆ là 
.
Khi đó phương trình tổng quát của đường thẳng ∆ đi qua điểm A(1; 2) và nhận 
làm VTPT là:
4(x – 1) + 3(y – 2) = 0
⇔ 4x + 3y – 10 = 0.
Vậy phương trình tổng quát của đường thẳng ∆ là 4x + 3y – 10 = 0.
b) Phương trình trục hoành là: y = 0.
Ta có M là giao điểm của ∆ và trục hoành nên điểm M thuộc trục hoành và thuộc đường thẳng ∆.
Vì M thuộc vào trục hoành nên gọi tọa độ điểm M là M(xM; 0).
Mà M cũng thuộc đường thẳng ∆ nên tọa độ điểm M thỏa mãn phương trình đường thẳng ∆ ta có:
4xM + 3.0 – 10 = 0
⇔ 4xM = 10
⇔ xM = 
Vậy tọa độ điểm M là 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao