Giải bài tập Bài 3 trang 57 Toán lớp 10 Tập 2 | Toán 10 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 57 Toán lớp 10 Tập 2. Bài 2: Đường thẳng trong mặt phẳng toạ độ. Toán 10 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 57 Toán lớp 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng ∆ trong các trường hợp sau:
a) ∆ đi qua A(2; 1) và song song với đường thẳng 3x + y + 9 = 0;
b) ∆ đi qua B(-1; 4) và vuông góc với đường thẳng 2x – y – 2 = 0.
Đáp án và cách giải chi tiết:
a) Đường thẳng 3x + y + 9 = 0 có vectơ pháp tuyến là
Do đường thẳng ∆ song song với đường thẳng 3x + y + 9 = 0 nên vectơ pháp tuyến của ∆ trùng với vectơ pháp tuyến của đường thẳng 3x + y + 9 = 0 là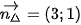 
Phương trình tổng quát của đường thẳng ∆ đi qua điểm A(2; 1) nhận 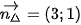làm VTPT là:
3(x – 2) + 1(y – 1) = 0
⇔ 3x + y – 7 = 0.
Ta có 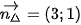là VTPT của đường thẳng ∆ nên VTCP của đường thẳng ∆ là 
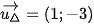. Khi đó phương trình tham số của đường thẳng ∆ đi qua điểm A(2; 1) và nhận 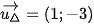làm VTCP: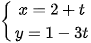 
Vậy Phương trình tổng quát của đường thẳng ∆ là 3x + y – 7 = 0 và phương trình tham số của đường thẳng ∆ là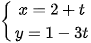
b) ∆ đi qua B(-1; 4) và vuông góc với đường thẳng 2x – y – 2 = 0.
Đường thẳng 2x – y – 2 = 0 có vectơ pháp tuyến là
Do đường thẳng ∆ vuông góc với đường thẳng 2x – y – 2 = 0 nên vectơ chỉ phương của ∆ trùng với vectơ pháp tuyến của đường thẳng 2x – y – 2 = 0 là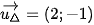 
Khi đó phương trình tham số của đường thẳng ∆ đi qua điểm B(-1; 4) và nhận 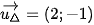làm VTCP: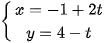 
Ta có 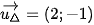là VTCP của đường thẳng ∆ nên VTPT của đường thẳng ∆ là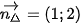 
Phương trình tổng quát của đường thẳng ∆ đi qua điểm A(-1; 4) nhận 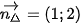làm VTPT là:
1(x + 1) + 2(y – 4) = 0
⇔ x + 2y – 7 = 0.
Vậy phương trình tổng quát của đường thẳng ∆ là x + 2y – 7 = 0 và phương trình tham số của đường thẳng ∆ là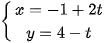
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao