Giải bài tập Bài 7.41 trang 65 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.41 trang 65 Toán 11 Tập 2. Bài tập cuối chương 7. Toán 11 - Kết nối tri thức
Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) (ABCD).
a) Tính theo a thể tích của khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AD và SC.
Đáp án và cách giải chi tiết:
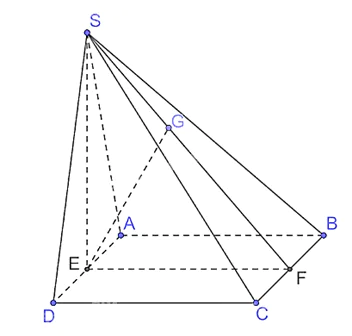
a) Kẻ SE ⊥ AD tại E. Vì tam giác SAD vuông cân tại S nên E là trung điểm của AD.
Có (SAD) ⊥ (ABCD), (SAD) ∩ (ABCD) = AD, SE ⊥ AD nên SE ⊥ (ABCD).
Vì tam giác SAD vuông cân tại S, SE là trung tuyến nên 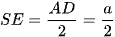
Khi đó 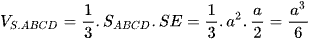
b) Do ABCD là hình vuông nên AD // BC mà BC ⊂ (SBC) nên AD // (SBC).
Khi đó d(AD, SC) = d(AD, (SBC)) = d(E, (SBC)).
Kẻ EF // AB (F thuộc BC). Khi đó EF ⊥ BC (vì AB ⊥ BC).
Mà SE ⊥ (ABCD) nên SE ⊥ BC mà EF ⊥ BC nên BC ⊥ (SEF).
Lại có BC ⊂ (SBC) nên (SBC) ⊥ (SEF) và (SBC) ∩ (SEF) = SF.
Kẻ EG ⊥ SF tại G nên EG ⊥ (SBC). Khi đó d(E, (SBC)) = EG.
Do ABCD là hình vuông nên EF = AB = a.
Xét tam giác SEF vuông tại E, EG là đường cao, có
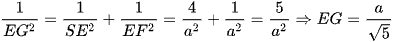
Vậy 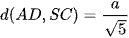 .
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao