Giải bài tập Bài 7.40 trang 65 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.40 trang 65 Toán 11 Tập 2. Bài tập cuối chương 7. Toán 11 - Kết nối tri thức
Đề bài:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a và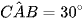 
. Biết SA ⊥ (ABC) và 
.
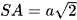a) Chứng minh rằng (SBC) ⊥ (SAB).
b) Tính theo a khoảng cách từ điểm A đến đường thẳng SC và khoảng cách từ điểm A đến mặt phẳng (SBC).
Đáp án và cách giải chi tiết:
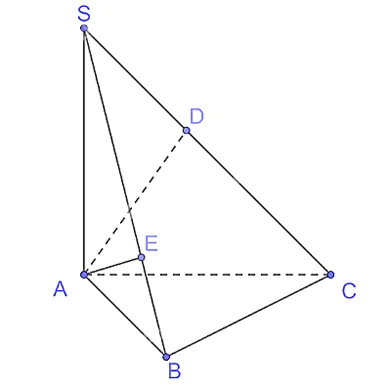
a) Do tam giác ABC vuông tại B nên AB ⊥ BC.
Vì SA ⊥ (ABC) nên SA ⊥ BC mà AB ⊥ BC nên BC ⊥ (SAB), suy ra (SBC) ⊥ (SAB).
b) Kẻ AD ⊥ SC tại D. Khi đó d(A, SC) = AD.
Vì SA ⊥ (ABC) nên SA ⊥ AC nên tam giác SAC vuông tại A.
Xét tam giác ABC vuông tại B,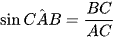 
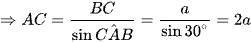
Xét tam giác SAC vuông tại A, AD là đường cao, có:
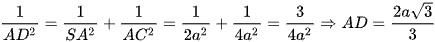
Vậy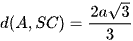 
.
Kẻ AE ⊥ SB tại E.
Vì BC ⊥ (SAB) nên BC ⊥ AE mà AE ⊥ SB nên AE ⊥ (SBC).
Khi đó d(A, (SBC)) = AE.
Xét tam giác ABC vuông tại B, có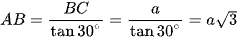 
Vì SA ⊥ (ABC) nên SA ⊥ AB, suy ra tam giác SAB vuông tại A.
Xét tam giác SAB vuông tại A, AE là đường cao, có:
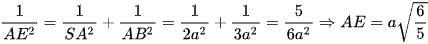
Vậy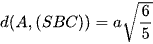 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao