Giải bài tập Bài 3 trang 64 Toán 11 Tập 2 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 64 Toán 11 Tập 2. Bài 2: Đường thẳng vuông góc với mặt phẳng. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng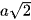 
, có các cạnh bên đều bằng 2a.
a) Tính góc giữa SC và AB.
b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD).
Đáp án và cách giải chi tiết:
a) Ta có: AB // CD ⇒ (SC, AB) = (SC, CD) =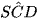 
Xét ΔSCD , áp dụng định lí cos, ta có:
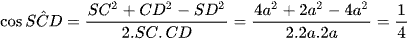
Do đó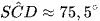 
.
b) Gọi O = AC ∩ BD
Ta có:
ΔSAC cân tại S nên SO ⊥ AC (1)
ΔSBD cân tại S nên SO ⊥ BD (2)
Từ (1) và (2) suy ra SO ⊥ (ABCD)
Do đó O là hình chiếu vuông góc của S lên (ABCD).
Mà A, B ∈ (ABCD)
Vậy ΔOAB là hình chiếu vuông góc của ΔSAB lên (ABCD).
Ta có: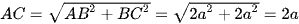 
Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.
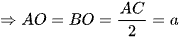
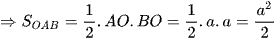
Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là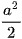 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao