Giải bài tập Bài 9 trang 11 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)

Hướng dẫn giải chi tiết từng bước bài tập Bài 9 trang 11 SBT Toán 12 Tập 1. Bài 1. Tính đơn điệu và cực trị của hàm số. SBT Toán 12 - Chân trời sáng tạo (SBT)

Đề bài:

Tìm m để phương trình x2+x+4x+1=m có hai nghiệm phân biệt.

Đáp án và cách giải chi tiết:

Đặt f(x) = x2+x+4x+1.

Tập xác định: D = ℝ\{−1}.

Ta có: f'(x) = (2x+1)(x+1)-x2-x-4(x+1)2=x2+2x-3(x+1)2

           f'(x) = 0 ⇔ x2+2x-3(x+1)2 = 0 ⇔ x = 1 hoặc x = −3.

Bảng biến thiên:

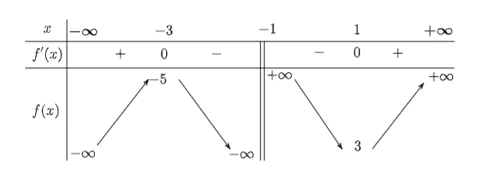
Xét sự tương giao của đồ thị hàm số y = x2+x+4x+1 và đường thẳng y = m, để phương trình có hai nghiệm phân biệt thì m < −5 hoặc m > 3.

Nguồn: giaitoanhay.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Giải bài tập SBT Toán 12 - Chân trời sáng tạo (SBT)

Xem tất cả Bài 1. Tính đơn điệu và cực trị của hàm số Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số Bài 3. Đường tiệm cận của đồ thị hàm số. Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản Bài tập cuối chương 1
Xem tất cả Bài 1. Vectơ và các phép toán trong không gian Bài 2. Toạ độ của vectơ trong không gian. Bài 3. Biểu thức toạ độ của các phép toán vectơ. Bài tập cuối chương 2
Xem tất cả Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm. Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm. Bài tập cuối chương 3
Xem tất cả Bài 1. Nguyên hàm. Bài 2. Tích phân. Bài 3. Ứng dụng hình học của tích phân. Bài tập cuối chương 4.
Xem tất cả Bài 1. Phương trình mặt phẳng Bài 2. Phương trình đường thẳng trong không gian Bài 3. Phương trình mặt cầu Bài tập cuối chương 5
Xem tất cả Bài 1. Xác suất có điều kiện Bài 2. Công thức xác suất toàn phần và công thức Bayes. Bài tập cuối chương 6