Giải bài tập Bài 4 trang 10 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 4 trang 10 SBT Toán 12 Tập 1. Bài 1. Tính đơn điệu và cực trị của hàm số. SBT Toán 12 - Chân trời sáng tạo (SBT)
Đề bài:
Xét tính đơn điệu và tìm cực trị của các hàm số:
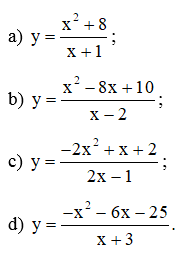
Đáp án và cách giải chi tiết:
a) y = .
Tập xác định: D = ℝ\{−1}.
Ta có: y' =
y' = 0 ⇔ x2 + 2x – 8 = 0 ⇔ x = 2 hoặc x = −4.
Ta có bảng biến thiên:

Hàm số đồng biến trên các khoảng (−∞; −4) và (2; +∞).
Hàm số nghịch biến trên các khoảng (−4; −1) và (−1; 2).
Hàm số đạt cực đại tại x = −4, yCĐ = −8.
Hàm số đạt cực tiểu tại x = 2, yCT = 4.
b) y = .
Tập xác định: D = ℝ\{2}.
Ta có: y' = .
Nhận thấy y' > 0, với mọi x ∈ D.
Ta có bảng biến thiên như sau:

Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).
Hàm số không có cực trị.
c) y = .
Tập xác định: D = ℝ\.
Ta có: y' = .
Nhận thấy y' < 0, với mọi x ∈ D.
Ta có bảng biến thiên:

Hàm số nghịch biến trên các khoảng .
Hàm số không có cực trị.
d) y = .
Tập xác định: D = ℝ\{−3}.
Ta có: y' =
y' = 0 ⇔ = 0 ⇔ x = 1 hoặc x = −7.
Bảng biến thiên:

Hàm số đồng biến trên các khoảng (−7; −3) và (−3; 1).
Hàm số nghịch biến trên các khoảng (−∞; −7) và (1; +∞).
Hàm số đạt cực đại tại x = 1, yCĐ = −8.
Hàm số đạt cực tiểu tại x = −7, yCT = 8.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao