Giải bài tập Bài 2.8 trang 58 Toán 12 Tập 1 | SGK Toán 12 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 2.8 trang 58 Toán 12 Tập 1. Bài 6. Vectơ trong không gian.. SGK Toán 12 - Kết nối tri thức
Đề bài:
Bài 2.8 trang 58 Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn , ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

Đáp án và cách giải chi tiết:
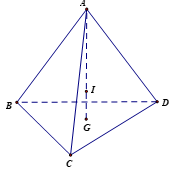
Giả sử khối rubik (đồng chất) hình tứ diện đều được mô phỏng như hình vẽ.
G là trọng tâm DBCD, I là trọng tâm của tứ diện
Vì ABCD là hình tứ diện đều nên AG(BCD) và AG = 8 cm.
Vì nên 3 điểm A, I, G thẳng hàng và .
Do đó IG (BCD). Khi đó cm.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao