Giải bài tập Luyện tập 5 trang 114 Toán 11 Tập 2 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 5 trang 114 Toán 11 Tập 2. Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối. Toán 11 - Cánh diều
Đề bài:
Cho khối tứ diện đều ABCD cạnh a. Chứng minh rằng thể tích của khối tứ diện đó bằng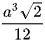 
.
Đáp án và cách giải chi tiết:
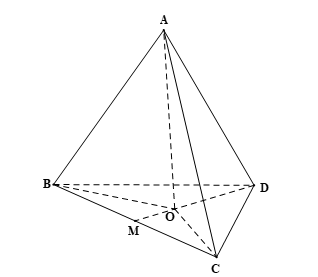
Gọi M là trung điểm của BC, O là trọng tâm tam giác BCD.
Vì ABCD là hình tứ diện đều nên BCD là tam giác đều.
Mà O là trọng tâm tam giác BCD nên O cũng là tâm đường tròn ngoại tiếp tam giác BCD.
Do đó AO ⊥ (BCD).
Xét tam giác đều BCD có: DM là đường trung tuyến (do M là trung điểm của BC) cũng đồng thời là đường cao của tam giác nên DM ⊥ BC.
Do M là trung điểm của BC nên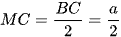 
Áp dụng định lí Pythagore vào tam giác DMC vuông tại M (do DM ⊥ BC) có:
DC2 = DM2 + MC2
Do đó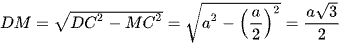 
Vì O là trọng tâm tam giác BCD nên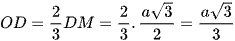 
Do AO ⊥ (BCD) và DO ⊂ (BCD) nên AO ⊥ DO, do đó tam giác ADO vuông tại O.
Áp dụng định lí Pythagore vào tam giác ADO vuông tại O có:
AD2 = AO2 + DO2
Suy ra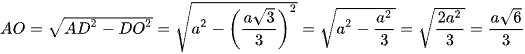 
Diện tích tam giác BCD đều có đường cao DM là:
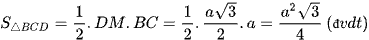
Thể tích của khối tứ diện đều ABCD cạnh a có chiều cao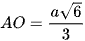 
và diện tích đáy 
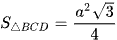là:
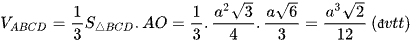
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao