Giải bài tập Hoạt động khám phá 3 trang 82 Toán 11 Tập 1 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 3 trang 82 Toán 11 Tập 1. Bài 3: Hàm số liên tục. Toán 11 - Chân trời sáng tạo
Đề bài:
Cho hai hàm số 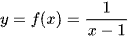 và
và 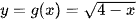 .
.
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số liên tục trên những khoảng nào? Giải thích.
Đáp án và cách giải chi tiết:
a) +) Xét hàm số: 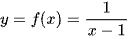
Điều kiện xác định của hàm số là x ≠ 1.
Vậy tập xác định của hàm số là: D = ℝ \ {1}.
+) Xét hàm số: 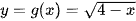
Điều kiện xác định của hàm số là: 4 – x ≥ 0 ⇔ x ≤ 4.
Vậy tập xác định của hàm số là: D = (– ∞; 4].
b) +) Xét hàm số f(x):
Với x0 ∈ ( – ∞; 1) thì 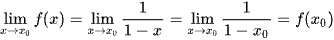
Suy ra hàm số f(x) liên tục trên (– ∞; 1).
Với x0 ∈ ( 1; + ∞) thì 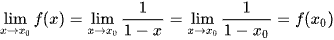
Suy ra hàm số f(x) liên tục trên (1; + ∞).
+) Xét hàm số g(x):
Với x0 ∈ (– ∞; 4) thì 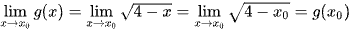
Tại x0 = 4 thì 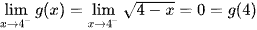
Vậy hàm số liên tục trên (– ∞; 4].
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao