Giải bài tập HĐ4 trang 40 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ4 trang 40 Toán 10 Tập 2. Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. Toán 10 - Kết nối tri thức
Đề bài:
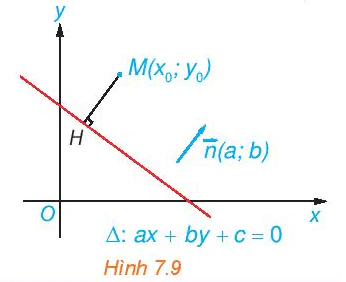
Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến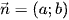 
. Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9).
a) Chứng minh rằng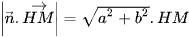 
.
b) Giả sử H có tọa độ (x1; y1). Chứng minh rằng: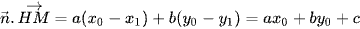 
.
c) Chứng minh rằng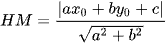 
.
Đáp án và cách giải chi tiết:
a) Do H là hình chiếu của M lên ∆ nên MH ⊥ ∆.
Vectơ 
là vectơ pháp tuyến của ∆ nên giá của vectơ vuông góc với ∆.
Khi đó đường thẳng MH song song hoặc trùng với giá của vectơ nên hai vectơ 
và cùng phương.
Do đó hai vectơ và cùng hướng hoặc ngược hướng.
+) Nếu hai vectơ và cùng hướng thì 
+) Nếu hai vectơ và ngược hướng thì 
Vậy 
.
b) Vì H thuộc ∆ nên tọa độ của H thỏa mãn phương trình ∆, thay tọa độ của H vào phương trình ∆ ta được: ax1 + by1 + c = 0 ⇔ c = – ax1 – by1 (1).
Ta lại có: 
Suy ra: 
(2).
Từ (1) và (2) suy ra: 
.
c) Theo câu a) ta có: 
Theo câu b) ta có: 
Suy ra: 
Vậy 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao