Giải bài tập Bài 7.10 trang 41 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.10 trang 41 Toán 10 Tập 2. Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. Toán 10 - Kết nối tri thức
Đề bài:
Bài 7.10 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(– 2; – 1).
a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.
b) Tính diện tích tam giác ABC.
Đáp án và cách giải chi tiết:
a) Độ dài đường cao kẻ từ đỉnh của tam giác ABC chính là khoảng cách từ điểm A đến đường thẳng BC.
Ta có: .
Chọn vectơ chỉ phương của đường thẳng BC là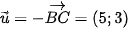 
Suy ra vectơ pháp tuyến của đường thẳng BC là
Đường thẳng BC đi qua điểm B(3; 2) và có vectơ pháp tuyến , do đó phương trình đường thẳng BC là: 3(x – 3) – 5(y – 2) = 0 hay 3x – 5y + 1 = 0.
Khi đó khoảng cách từ A đến BC là: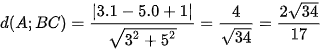
Vậy độ dài đường cao kẻ từ đỉnh A của tam giác ABC là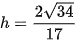 
b) Ta có: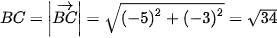
Diện tích tam giác ABC là: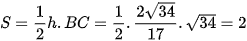 
(đvdt)
Vậy diện tích tam giác ABC là 2 đvdt.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao