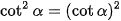Giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0° đến 180° | Kết Nối Tri Thức
Hướng dẫn giải chi tiết Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°
Bài 3.1 trang 37 Toán 10 Tập 1
Bài 3.1 trang 37 Toán 10 Tập 1: Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:
a) 
;
b)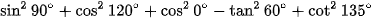 
;
c)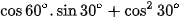 
.
Chú ý:
, 
Bài 3.2 trang 37 Toán 10 Tập 1
Bài 3.2 trang 37 Toán 10 Tập 1: Đơn giản các biểu thức sau:
a) sin1000 + sin800 + cos160 + cos 1640;
b) 2sin(1800 – α)cotα – cos(1800 – α).tanα.cos(1800 – α) với 00 < α < 900.
Bài 3.3 trang 37 Toán 10 Tập 1
Bài 3.3 trang 37 Toán 10 Tập 1: Chứng minh các hệ thức sau:
a)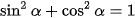 
;
b)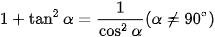 
;
c)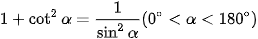 
Bài 3.4 trang 37 Toán 10 Tập 1
Bài 3.4 trang 37 Toán 10 Tập 1: Cho góc thỏa mãn
Tính giá trị của biểu thức:
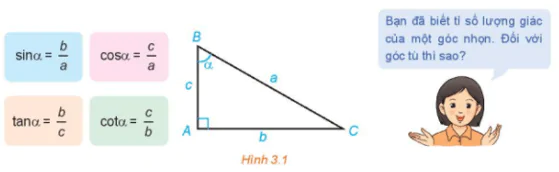
HĐ1 trang 34 Toán 10 Tập 1
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
α = 90°;
α < 90°;
α > 90°;
b) Khi 0° < α < 90°, nêu mối quan hệ giữa cosα, sinα với hoành độ và tung độ của điểm M.
Luyện tập 1 trang 35 Toán 10 Tập 1
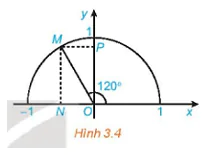
Tìm các giá trị lượng giác của góc 1200 (H.3.4).
HĐ2 trang 36 Toán 10 Tập 1
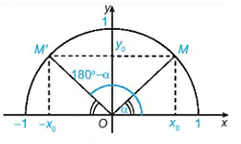
Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa sinα và sin(180° - α), giữa cosα và cos(180° - α).
Luyện tập 2 trang 36 Toán 10 Tập 1
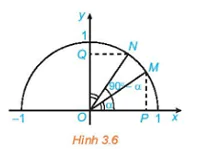
Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau α và 90° - α 
. Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa cosα và sin(90° - α).
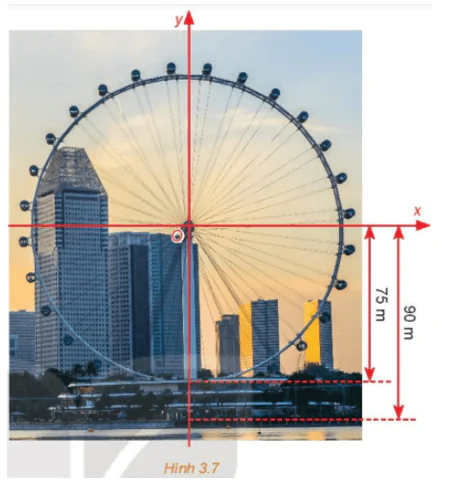
Vận dụng trang 37 Toán 10 Tập 1
Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào Cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?
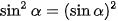
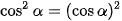
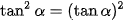