Giải bài tập Bài 7 trang 74 Toán lớp 10 Tập 2 | Toán 10 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 7 trang 74 Toán lớp 10 Tập 2. Bài tập cuối chương 9. Toán 10 - Chân trời sáng tạo
Đề bài:
Bài 7 trang 74 Toán lớp 10 Tập 2: Lập phương trình đường tròn trong các trường hợp sau:
a) Có tâm I(-2; 4) và bán kính bằng 9;
b) Có tâm I(1; 2) và đi qua điểm A(4; 5);
c) Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y – 16 = 0;
d) Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.
Đáp án và cách giải chi tiết:
a) Phương trình có tâm I(-2; 4) và bán kính bằng 9 là:
(x + 2)2 + (y – 4)2 = 92
⇔ x2 + 4x + 4 + y2 – 8y + 16 = 81
⇔ x2 + y2 + 4x – 8y – 61 = 0
Vậy phương trình đường tròn cần tìm là x2 + y2 + 4x – 8y – 61 = 0.
b) Ta có: 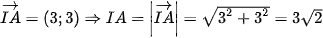
Đường tròn cần tìm có tâm I và đi qua điểm A nên độ dài đoạn thẳng IA bằng bán kính của đường tròn nên 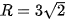
Phương trình đường tròn tâm I(1; 2) và bán kính 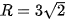 là:
là:
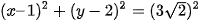
⇔ (x – 1)2 + (y – 2)2 = 18
Vậy phương trình đường tròn cần tìm là (x – 1)2 + (y – 2)2 = 18.
c) Xét phương trình đường thẳng 4x + y – 16 = 0 đi qua điểm M(4; 0) có VTPT là khi đó VTCP của đường thẳng là
Phương trình tham số của đường thẳng là: 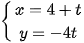
Gọi I là tâm của đường tròn cần tìm.
Vì I nằm trên đường thẳng 4x + y – 16 = 0 nên I(4 + t; -4t).
Ta có: 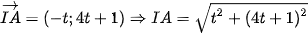
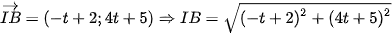
Vì đường tròn đi qua hai điểm A và B nhận I làm tâm nên IA = IB = R.
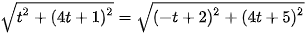
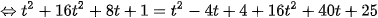
Phương trình đường tròn tâm I(3; 4) và có bán kính 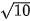 là:
là:
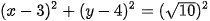
⇔ (x – 3)2 + (y – 4)2 = 10.
Vậy phương trình đường tròn cần tìm là (x – 3)2 + (y – 4)2 = 10.
d) Gọi A, B là giao điểm của đường tròn cần tìm với lần lượt trục Ox và Oy.
Ta có hình vẽ sau:

Kẻ OH ⊥ Ox, OK ⊥ Oy
⇒ H là trung điểm của OA (đường kính vuông góc với dây) ⇒ OH = HA =
⇒ K là trung điểm của OB (đường kính vuông góc với dây) ⇒ OK = KB =
⇒
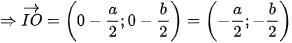
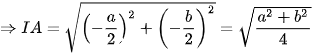
Phương trình đường tròn cần tìm là:
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao