Giải bài tập Bài 2 trang 25 Toán 9 Tập 1 | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 25 Toán 9 Tập 1. Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn.. Toán 9 - Cánh diều
Đề bài:
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a. 
b. 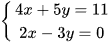
c. 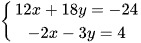
d. 
Đáp án và cách giải chi tiết:
a) Giải phương trình: 
Cộng từng vế hai phương trình của hệ trên, ta nhận được phương trình: 3x = 6. (1)
Giải phương trình (1):
3x = 6
x = 2.
Thay x = 2 vào phương trình thứ hai, ta có: 2 – y = 2, tức là y = 0.
Vậy hệ phương trình có nghiệm (2;0)
b) Giải phương trình: 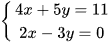
Nhân hai vế của phương trình thứ hai với 2, ta được hệ phương trình sau:

Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta nhận được phương trình:
5y – (–6y) = 11. (2)
Giải phương trình (2):
5y – (–6y) = 11
5y + 6y = 11
11y = 11
y = 1.
Thay y = 1 vào phương trình 2x – 3y = 0, ta có: 2x – 3.1 = 0. (3)
Giải phương trình (3):
2x – 3.1 = 0
2x – 3 = 0
2x = 3
Vậy hệ phương trình đã cho có nghiệm duy nhất (
c) Giải phương trình: 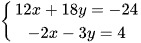
Nhân hai vế của phương trình thứ hai với 6, ta được hệ phương trình sau:

Cộng từng vế hai phương trình của hệ trên, ta được phương trình:
0x + 0y = 0, hay 0x = 0. Phương trình này có vô số nghiệm x ∈ ℝ.
Từ phương trình thứ hai ta có 3y = –2x – 4, suy ra
Vậy hệ phương trình đã cho có vô số nghiệm 
d) Giải phương trình: 
Chia hai vế của phương trình thứ hai cho 2, ta được hệ phương trình sau:

Cộng từng vế hai phương trình của hệ trên, ta được phương trình:
0x + 0y = 10, hay 0x = 10. Phương trình này vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao