Giải bài tập Toán 9 Bài 3. Định lí Viète. | Cánh Diều
Hướng dẫn giải chi tiết Bài 3. Định lí Viète. Tìm hai số khi biết tổng và tích.
Khởi động trang 61 Toán 9 Tập 2:
Đà Lạt là thành phố du lịch, có khí hậu mát mẻ. Nơi đây trồng nhiều loại hoa để phục vụ nhu cầu trong nước và xuất khẩu. Giả sử người ta trồng hoa trên một mảnh vườn có dạng hình chữ nhật với diện tích là 240 m2, chu vi là 68 m

Làm thế nào để xác định được chiều dài, chiều rộng của mảnh vườn trồng hoa nói trên?
Hoạt động 1 trang 61 Toán 9 Tập 2:
Xét phương trình ax2 + bx + c = 0 (a ≠ 0). Giả sử phương trình đó có hai nghiệm là x1, x2. Tính x1 + x2; x1x2 theo các hệ số a, b, c.
Luyện tập 1 trang 62 Toán 9 Tập 2:
Cho phương trình: – 4x2 + 9x + 1 = 0.
a) Chứng minh phương trình có hai nghiệm phân biệt x1, x2.
b) Tính x1 + x2 ; x1x2.
c) Tính
Luyện tập 2 trang 63 Toán 9 Tập 2:
Không tính ∆, giải phương trình 4x2 – 7x + 3 = 0
Luyện tập 3 trang 63 Toán 9 Tập 2:
Không tính ∆, giải phương trình
2x2 – 9x – 11 = 0.
Hoạt động 2 trang 63 Toán 9 Tập 2:
Cho hai số có tổng bằng 5 và tích bằng 6.
a) Gọi một số là x. Tính số còn lại theo x.
b) Lập phương trình bậc hai ẩn x.
Bài 1 trang 64 Toán 9 Tập 2:
Nếu x1, x2 là hai nghiệm của phương trình ax2 + bx + c (a ≠ 0) thì
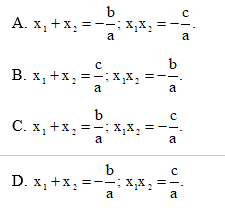
Bài 2 trang 64 Toán 9 Tập 2:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu phương trình ax2 + bx + c (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
b) Nếu phương trình ax2 + bx + c (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x1 = –1 và nghiệm còn lại là
c) Nếu phương trình ax2 + bx + c (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm là x1 = –1 và nghiệm còn lại là
d) Nếu phương trình ax2 + bx + c (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1 và nghiệm còn lại là
Bài 3 trang 64 Toán 9 Tập 2:
Giải thích vì sao nếu ac < 0 thì phương trình ax2 + bx + c (a ≠ 0) có hai nghiệm là hai số trái dấu nhau.
Bài 4 trang 64 Toán 9 Tập 2:
Cho phương trình 2x2 – 3x – 6 = 0.
a) Chứng minh phương trình có hai nghiệm phân biệt x1, x2.
b) Tính x1 + x2; x1x2. Chứng minh cả hai nghiệm x1, x2 đều khác 0.
c) Tính
d) Tính
e) Tính |x1 – x2|.
Bài 5 trang 65 Toán 9 Tập 2:
Không tính ∆, giải các phương trình:
a) 3x2 – x – 2 = 0;
b) –4x2 + x + 5 = 0;
c)
d)
Bài 6 trang 65 Toán 9 Tập 2:
Tìm hai số trong mỗi trường hợp sau:
a) Tổng của chúng bằng 7 và tích của chúng bằng 12;
b) Tổng của chúng bằng 1 và tích của chúng bằng –6.
Bài 7 trang 65 Toán 9 Tập 2:
Bác Đạt muốn thiết kế cửa sổ có dạng hình chữ nhật với diện tích bằng 2,52 m2 và chu vi bằng 6,4 m. Tìm các kích thước của cửa sổ đó.