Giải bài tập Thực hành 3 trang 32 Toán 12 Tập 1 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Thực hành 3 trang 32 Toán 12 Tập 1. Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản.. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = x - 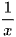 ;
;
b) y = -x + 2 -  ;
;
c) y =  .
.
Đáp án và cách giải chi tiết:
a) y = x - 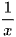
1. Tập xác định: D = ℝ\{0}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = 1 +  . Vì y' > 0 với mọi x ≠ 0 nên hàm số đồng biến trên mỗi khoảng (– ∞; 0) và (0; + ∞).
. Vì y' > 0 với mọi x ≠ 0 nên hàm số đồng biến trên mỗi khoảng (– ∞; 0) và (0; + ∞).
● Các giới hạn tại vô cực và tiệm cận:
 .
.
Ta có  .
.
 .
.
Suy ra đường thẳng y = x là tiệm cận xiên của đồ thị hàm số.
Ta có  . Suy ra đường thẳng x = 0 (hay trục Oy) là tiệm cận đứng của đồ thị hàm số.
. Suy ra đường thẳng x = 0 (hay trục Oy) là tiệm cận đứng của đồ thị hàm số.
● Bảng biến thiên:

3. Đồ thị:
Ta có y = 0 ⇔ x - 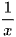 = 0 ⇔ x2 = 1 ⇔ x = – 1 hoặc x = 1.
= 0 ⇔ x2 = 1 ⇔ x = – 1 hoặc x = 1.
Vậy đồ thị hàm số giao với trục Ox tại điểm (– 1; 0) và điểm (1; 0).
Đồ thị hàm số không cắt trục Oy.
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là gốc tọa độ O(0; 0). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 0 (trục Oy) và y = x.
b) y = -x + 2 - 
1. Tập xác định: D = ℝ\{– 1}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = -1 +  . Ta có y' = 0 ⇔ x = – 2 hoặc x = 0.
. Ta có y' = 0 ⇔ x = – 2 hoặc x = 0.
Trên các khoảng (– ∞; – 2) và (0; + ∞), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
Trên các khoảng (– 2; – 1) và (– 1; 0), y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.
● Cực trị:
Hàm số đạt cực tiểu tại x = – 2 và yCT = 5.
Hàm số đạt cực đại tại x = 0 và yCĐ = 1.
● Các giới hạn tại vô cực và tiệm cận:
 .
.
Ta có  .
.
 .
.
Suy ra đường thẳng y = – x + 2 là tiệm cận xiên của đồ thị hàm số.
Ta có  . Suy ra đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
. Suy ra đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
● Bảng biến thiên:

3. Đồ thị:
Ta có y = 0 ⇔ -x + 2 -  = 0 ⇔ x =
= 0 ⇔ x =  hoặc x =
hoặc x =  .
.
Vậy đồ thị hàm số giao với trục Ox tại điểm  và điểm
và điểm  .
.
Đồ thị hàm số giao với trục Oy tại điểm (0; 1).
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là điểm I(– 1; 3).
Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = – 1 và y = – x + 2.
c) y = 
1. Tập xác định: D = ℝ\{– 1}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' =  . Vì y' < 0 với mọi x ≠ – 1 nên hàm số nghịch biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
. Vì y' < 0 với mọi x ≠ – 1 nên hàm số nghịch biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
● Các giới hạn tại vô cực và tiệm cận:
 .
.
Ta có  và
và  .
.
Suy ra đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số.
Ta có  . Suy ra đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
. Suy ra đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
● Bảng biến thiên:

3. Đồ thị:
Ta có y = 0 ⇔  = 0 ⇔ x = – 2 hoặc x = 1.
= 0 ⇔ x = – 2 hoặc x = 1.
Vậy đồ thị hàm số giao với trục Ox tại điểm (– 2; 0) và điểm (1; 0).
Đồ thị hàm số giao với trục Oy tại điểm (0; 2).
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là điểm I(– 1; 1).
Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = – 1 và y = – x.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao