Giải bài tập Luyện tập 5 trang 51 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 5 trang 51 Toán 11 Tập 2. Bài 25: Hai mặt phẳng vuông góc. Toán 11 - Kết nối tri thức
Đề bài:
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng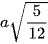 
. Tính số đo góc nhị diện [S, BC, A].
Đáp án và cách giải chi tiết:
Gọi G là hình chiếu của S trên mặt phẳng (ABC).
Vì S.ABC là hình chóp tam giác đều nên G là trọng tâm của tam giác ABC.
Gọi AG cắt BC tại D mà ABC là tam giác đều nên AD ⊥ BC.
Mà SG ⊥ (ABC) nên SG ⊥ BC.
Vì AD ⊥ BC và SG ⊥ BC nên BC ⊥ (SAD), suy ra BC ⊥ SD.
Vì AD ⊥ BC và BC ⊥ SD nên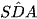 
là góc phẳng nhị diện của góc nhị diện [S, BC, A].
Vì ABC là tam giác đều cạnh a, AD là đường cao nên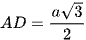 
.
Suy ra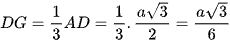 
Xét tam giác ABC có AD là trung tuyến nên D là trung điểm của BC, do đó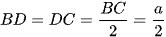 
.
Xét tam giác SBD vuông tại D có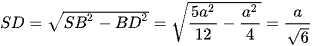 
Xét tam giác SGD vuông tại G có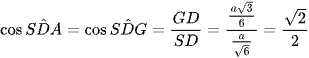 
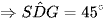
Vậy số đo góc nhị diện [S, BC, A] là 45°.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao