Giải bài tập HĐ12 trang 51 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ12 trang 51 Toán 11 Tập 2. Bài 25: Hai mặt phẳng vuông góc. Toán 11 - Kết nối tri thức
Đề bài:
Cho hình chóp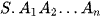 
. Gọi O là hình chiếu của S trên mặt phẳng 
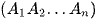(H.7.67).
a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều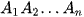 
?
b) Nếu đa giác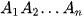 
là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?
Đáp án và cách giải chi tiết:
a) Do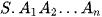 
là hình chóp đều nên SA1 = SA2 = … = SAn
Vì O là hình chiếu của S trên mặt phẳng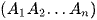 
nên SO ⊥ 
.
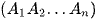Xét tam giác SOA1 vuông tại O, có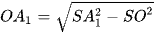 
;
Xét tam giác SOA2 vuông tại O, có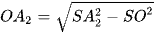 
;
…..
Xét tam giác SOAn vuông tại O, có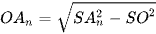 
.
Mà SA1 = SA2 = … = SAn nên OA1 = OA2 = … = OAn hay O là tâm đa giác đều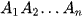 
.
b) Nếu đa giác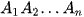 
là đều và O là tâm của đa giác đó thì OA1 = OA2 = … = OAn .
Vì O là hình chiếu của S trên mặt phẳng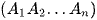 
nên SO ⊥ 
.
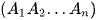Xét tam giác SOA1 vuông tại O, có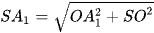 
;
Xét tam giác SOA2 vuông tại O, có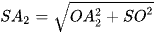 
;
…..
Xét tam giác SOAn vuông tại O, có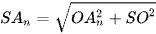 
.
Mà OA1 = OA2 = … = OAn nên SA1 = SA2 = … = SAn .
Vậy hình chóp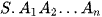 
là hình chóp đều.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao