Giải bài tập Bài 8 trang 37 SBT Toán 12 Tập 1 | SBT Toán 12 - Chân trời sáng tạo (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 8 trang 37 SBT Toán 12 Tập 1. Bài tập cuối chương 1. SBT Toán 12 - Chân trời sáng tạo (SBT)
Đề bài:
Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm3 với yêu cầu dùng ít vật liệu nhất.
Chiều cao hộp là 8 cm, các kích thước khác là x (cm), y (cm) với x > 0 và y > 0.
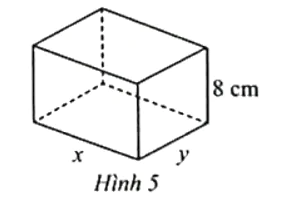
a) Chứng tỏ rằng y = .
b) Tìm diện tích toàn phần S(x) của chiếc hộp theo x.
c) Khảo sát hàm số S(x) trên khoảng (0; +∞).
d) Tìm kích thước của hộp để tiết kiệm vật liệu nhất. (Làm tròn kết quả đến hàng đơn vị của mi-li-mét).
Đáp án và cách giải chi tiết:
a) Ta có: V = 800 = 8xy ⇒ y = .
b) Diện tích toàn phần của chiếc hộp là:
S(x) = 2(x + y).8 + 2xy = 16(x + ) + 2x. = 16x + + 200.
c) S(x) = 16x + + 200, với x > 0.
S'(x) = 16 –
S'(x) = 0 ⇔ x2 = 100 ⇔ x = 10.
Bảng biến thiên:

Hàm số đồng biến trên (10; +∞), hàm số nghịch biến trên khoảng (0; 10).
d) Khi x = 10 thì hàm số S(x) đạt giá trị nhỏ nhất và S(10) = 520.
Lúc này, y = = 10, nghĩa là khi làm đáy hộp là hình vuông có cạnh bằng 10 cm thì sẽ tiết kiệm vật liệu nhất.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao