Giải bài tập Bài 6.17 trang 24 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 6.17 trang 24 Toán 10 Tập 2. Bài 17: Dấu của tam thức bậc hai. Toán 10 - Kết nối tri thức
Đề bài:
Bài 6.17 trang 24 Toán 10 Tập 2: Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi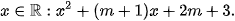 
Đáp án và cách giải chi tiết:
Ta có tam thức f(x) = x2 + (m + 1)x + 2m + 3 có ∆ = (m + 1)2 – 4 . 1 . (2m + 3) = m2 + 2m + 1 – 8m – 12 = m2 – 6m – 11.
Lại có hệ số a = 1 > 0.
Để f(x) luôn dương (cùng dấu hệ số a) với mọi thì ∆ < 0.
⇔ m2 – 6m – 11 < 0.
Xét tam thức h(m) = m2 – 6m – 11 có ∆'m = (– 3)2 – 1 . (– 11) = 20 > 0 nên h(m) có hai nghiệm 
và 
Mặt khác ta có hệ số am = 1 > 0, do đó ta có bảng xét dấu sau:
Do đó, h(m) < 0 với mọi 
Hay ∆ < 0 với mọi 
Vậy thì tam thức bậc hai đã cho luôn dương với mọi
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao