Giải bài tập Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2 | Toán 10 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2. Bài 4: Ba đường conic trong mặt phẳng toạ độ. Toán 10 - Chân trời sáng tạo
Đề bài:
Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2: Cho hypebol (H) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Điểm M thuộc hypecbol (H) khi và chỉ khi |F1M – F2M| = 2a. Chọn hệ trục tọa độ Oxy sao cho F1(-c; 0) và F2(c; 0). Xét điểm M(x; y).
a) Tính F1M và F2M theo x, y và c.
b) Giải thích các phát biểu sau:
M(x; y) ∈ (H) ⇔ 
Đáp án và cách giải chi tiết:
a) Ta có: 
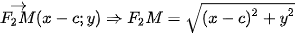
Vậy 
và 
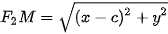
b) +) Ta có: Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F1M + F2M = 2a.
Nếu M thuộc elip (E) thì F1M + F2M = 2a hay 
+) Nếu điểm M(x; y) có tọa độ thỏa mãn hay F1M + F2M = 2a thì M là điểm thỏa mãn F1M + F2M = 2a.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao