Giải bài tập Bài 7 trang 82 Toán 11 Tập 2 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 7 trang 82 Toán 11 Tập 2. Bài 4: Khoảng cách trong không gian. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 7 trang 82 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng AC và SB.
b) Tính thể tích của khối chóp.
Đáp án và cách giải chi tiết:
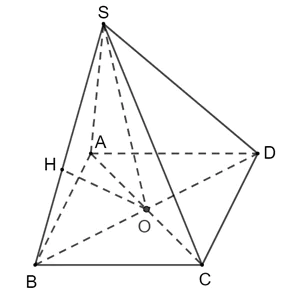
a) Kẻ OH ⊥ SB (H ∈ SB)
S.ABCD là hình chóp tứ giác đều ⇒ SO ⊥ (ABCD) ⇒ SO ⊥AC.
Tứ giác ABCD là hình vuông suy ra AC ⊥ BD ⇒ AC ⊥(SBD) ⇒ AC ⊥ OH.
Mà OH ⊥ SB
Do đó d(AC, SB) = OH
• Xét ΔABD vuông tại A, ta có:
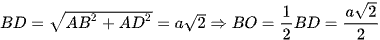
• Xét ΔSBO vuông tại O, ta có:
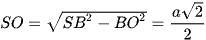
• Xét ΔSBO vuông tại O có SO = BO nên ΔSBO vuông cân tại O
Suy ra OH vừa là đường cao, vừa là đường trung tuyến.
Do đó 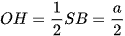
Vậy d(AC, SB) = 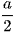 .
.
b) 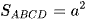
Thể tích khối chóp là: 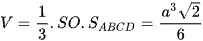
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao