Giải bài tập Bài 5.16 trang 122 Toán 11 Tập 1 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 5.16 trang 122 Toán 11 Tập 1. Bài 17: Hàm số liên tục. Toán 11 - Kết nối tri thức
Đề bài:
Tìm giá trị của tham số m để hàm số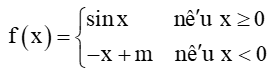
liên tục trên ℝ.
Đáp án và cách giải chi tiết:
Tập xác định của hàm số là ℝ.
+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên .
+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên .
Khi đó, hàm số f(x) liên tục trên các khoảng .
Do đó, để hàm số f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0. Điều này xảy ra khi và chỉ khi
Lại có:
Khi đó, (1) ⇔ m = 0.
Vậy m = 0 thì thỏa mãn yêu cầu bài toán.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Loading...