Giải bài tập Bài 7.14 trang 47 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.14 trang 47 Toán 10 Tập 2. Bài 21: Đường tròn trong mặt phẳng tọa độ. Toán 10 - Kết nối tri thức
Đề bài:
Bài 7.14 trang 47 Toán 10 Tập 2: Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a)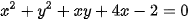 
;
b)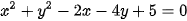 
;
c)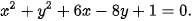 
Đáp án và cách giải chi tiết:
a) Phương trình 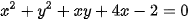không có dạng x2 + y2 – 2ax – 2by + c = 0 với a, b, c là các số thực nên đây không phải phương trình đường tròn.
b) x2 + y2 – 2x – 4y + 5 = 0 ⇔ x2 + y2 – 2 . 1 . x – 2 . 2 . y + 5 = 0.
Các hệ số: a = 1, b = 2, c = 5.
Ta có: a2 + b2 – c = 12 + 22 – 5 = 0 nên đây cũng không phải phương trình đường tròn.
c) x2 + y2 + 6x – 8y + 1 = 0 ⇔ x2 + y2 – 2 . (– 3) . x – 2 . 4 . y + 1 = 0.
Các hệ số: a = – 3, b = 4, c = 1.
Ta có: a2 + b2 – c = (– 3)2 + 42 – 1 = 24 > 0 nên đây là phương trình đường tròn.
Đường tròn này có tâm I(– 3; 4) và bán kính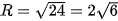 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao