Giải bài tập Bài 5 trang 94 Toán 8 Tập 2 | Toán 8 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 94 Toán 8 Tập 2. Bài tập cuối chương VIII.. Toán 8 - Cánh diều
Đề bài:
Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
a) MP // AD,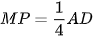 
;
b)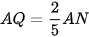 
c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và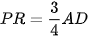 
.
Đáp án và cách giải chi tiết:
a) Do N là trung điểm của BC nên 
Và ABCD là hình bình hành nên BC = AD, BC // AD
Suy ra 
(1)
Xét ∆ABN có M, P lần lượt là trung điểm của AB, AN nên MP là đường trung bình của ∆ABN
Suy ra 
và MP // BN (2)
Từ (1) và (2) ta có 
và MP // AD.
Vậy MP // AD và 
(3)
b) Xét ∆ADQ với MP // AD, ta có 
(hệ quả của định lí Thalès)
Hay 
nên 
Suy ra 
hay 
Mà P là trung điểm của AN nên 
Do đó 
suy ra 
Vậy 
c) Gọi K là trung điểm của DN.
Xét ∆AND có P, K lần lượt là trung điểm của AN, DN nên PK là đường trung bình của ∆AND. Do đó PK // AD và 
(4)
Tương tự, xét ∆CDN có KR là đường trung bình của ∆CDN nên KR // CN và 
Mà N là trung điểm của BC nên 
và BC // AD
Do đó KR // AD và 
(5)
Từ (3), (4) và (5), theo tiên đề Euclid ta có: M, P, K, R thẳng hàng.
Và 
Vậy ba điểm M, P, R thẳng hàng và 
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao