Giải bài tập Bài 4 trang 15 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 4 trang 15 Toán 11 Tập 1. Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác. Toán 11 - Cánh diều
Đề bài:
Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:
a)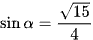 
với 
;
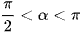b)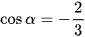 
với ‒π < α < 0;
c) tanα = 3 với ‒π < α < 0;
d) cotα = ‒2 với 0 < α < π.
Đáp án và cách giải chi tiết:
a) Do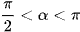 
nên cosα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:
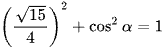
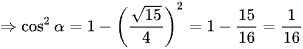
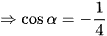(do cosα < 0).
Ta có: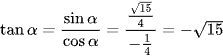 
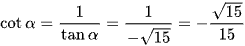
Vậy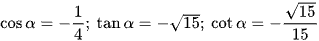 
b) Do ‒π < α < 0 nên sinα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:
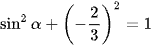
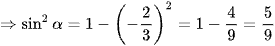
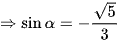(do sinα < 0).
Ta có: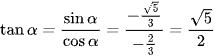 
;
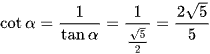
Vậy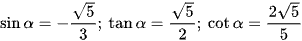 
c) Do ‒π < α < 0 nên sinα < 0 và cosα > 0 khi khi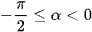 
, cosα < 0 khi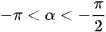 
Mà tanα = 3 > 0, do đó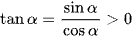 
, từ đó suy ra cosα < 0.
Áp dụng công thức tanα.cotα = 1, ta có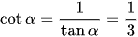 
Áp dụng công thức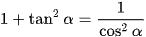 
, ta có:
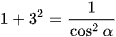hay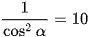 
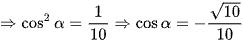(do cosα < 0).
Áp dụng công thức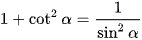 
, ta có:
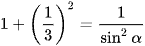hay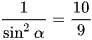 
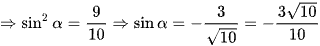(do sinα < 0).
Vậy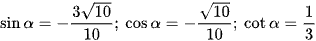 
d) cotα = ‒2 với 0 < α < π.
Áp dụng công thức tanα.cotα = 1, ta có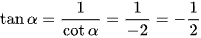 
Do 0 < α < π nên sinα > 0.
Mà cotα = ‒2 < 0 nên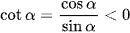 
, suy ra cosα < 0.
Áp dụng công thức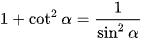 
, ta có:
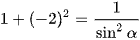hay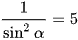 
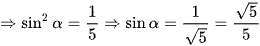(do sinα > 0).
Ta có: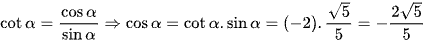 
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao