Giải bài tập Bài 12 trang 121 Toán 8 Tập 1 | Toán 8 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 12 trang 121 Toán 8 Tập 1. Bài tập cuối chương 5 Tam giác tứ giác. Toán 8 - Cánh diều
Đề bài:
Bài 12 trang 121 Toán 8 Tập 1: Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a)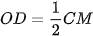 
và tam giác ACM là tam giác vuông;
b) Ba điểm A, D, M thẳng hàng;
c) Tam giác DCM là tam giác cân.
Đáp án và cách giải chi tiết:
a) • Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Suy ra 
Do BCMD là hình bình hành nên BD = CM.
Do đó 
• Ta có: CM // BD (do BCMD là hình bình hành)
AC ⊥ BD (chứng minh trên)
Do đó CM ⊥ AC hay 
Vây tam giác ACM là tam giác vuông.
b) Vì ABCD là hình thoi nên AD // BC
Vì BCMD là hình bình hành nên DM // BC
Do đó qua điểm D có hai đường thẳng AD và DM cùng song song với đường thẳng BC nên AD trùng với DM (Tiên đề Euclid)
Hay ba điểm A, D, M thẳng hàng.
c) Ta có: BD // CM (chứng minh câu a) nên:
• 
(so le trong); (1)
• 
(đồng vị) (2)
Do ABCD là hình thoi nên DB là tia phân giác của góc ADC
Do đó 
(3)
Từ (1), (2) và (3) suy ra 
Xét ΔDCM có nên là tam giác cân tại D.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao