Giải bài tập Luyện tập 2 trang 99 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 2 trang 99 Toán 11 Tập 1. Bài 2: Hai đường thẳng song song trong không gian. Toán 11 - Cánh diều
Đề bài:
Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).
Đáp án và cách giải chi tiết:
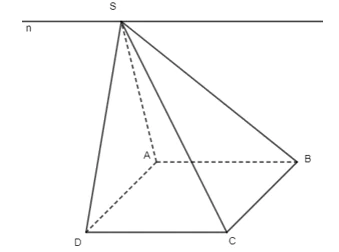
• Ta có: S ∈ (SAB) và S ∈ (SCD) nên S là giao điểm của (SAB) và (SCD).
Mà AB // CD;
AB ⊂ (SAB);
CD ⊂ (SCD).
Do đó giao tuyến của (SAB) và (SCD) là đường thẳng n đi qua S và song song với AB và CD.
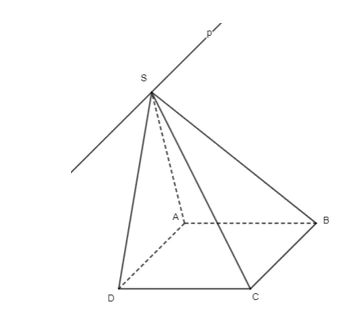
• Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).
Mà AD // BC
AD ⊂ (SAD);
BC ⊂ (SBC).
Do đó giao tuyến của (SAD) và (SBC) là đường thẳng p đi qua S và song song với AD và BC.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao