Giải bài tập Hoạt động 1 trang 65 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 1 trang 65 Toán 11 Tập 1. Bài 2: Giới hạn của hàm số. Toán 11 - Cánh diều
Đề bài:
Xét hàm số f(x) = 2x.
a) Xét dãy số (xn), với xn = 1 + . Hoàn thành bảng giá trị f(xn) tướng ứng.

Các giá trị tương ứng của hàm số f(x1), f(x2), ..., f(xn), ... lập thành một dãy số mà ta kí hiệu là (f(xn)). Tìm limf(xn).
b) Chứng minh rằng với dãy số bất kì (xn), xn → 1 ta luôn có f(xn) → 2.
Đáp án và cách giải chi tiết:
a) Ta có bảng giá trị sau:
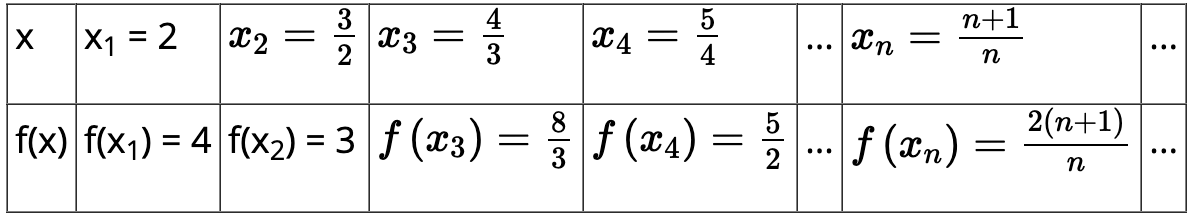
Ta có: limf(xn) = lim = 2.
b) Lấy dãy (xn) bất kí thỏa mãn xn → 1 ta có:
f(xn) = 2xn
⇒ limf(xn) = lim2xn = 2lim xn = 2.1 = 2.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Loading...
Bài tập liên quan:
Giải bài tập Toán 11 - Cánh diều
Xem tất cả
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
Bài tập cuối chương 4