Giải bài tập Bài 9 trang 86 Toán 11 Tập 2 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 9 trang 86 Toán 11 Tập 2. Bài tập cuối chương 8. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 9 trang 86 Toán 11 Tập 2: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD.
a) Chứng minh rằng (SMD) ⊥ (SNC).
b) Tính khoảng cách từ M đến mặt phẳng (SNC).
Đáp án và cách giải chi tiết:
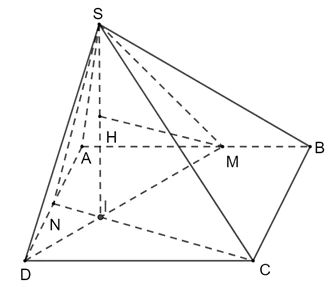
a) Tam giác SAB đều có M là trung điểm AB nên SM ⊥ AB. Mà (SAB) ⊥ (SAB) nên SM ⊥ (ABCD). Suy ra SM ⊥ NC.
Xét ΔAMD và ΔDNC
AM = DN
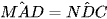
AD = DC
Do đó ΔAMD và ΔDNC (c.g.c)
Suy ra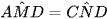 
(hai góc tương ứng)
Mà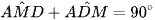 
nên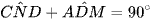 
Từ đó ta có tam giác DNI vuông tại I hay DM ⊥ NC. Mà SM ⊥ NC nên NC ⊥ (SND).
Vậy (SNC) ⊥ (SMD).
b) Kẻ MH ⊥ SI (H ∈ SI).
Vì NC ⊥ (SMD) ⇒ NC ⊥ MH ⇒ MH ⊥ (SNC)
Tam giác SAB đều có SM là trung tuyến nên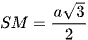 
Tam giác CND vuông có DI là đường cao nên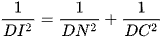 
Suy ra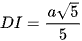 
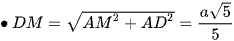
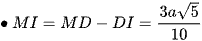
Và SM ⊥ (ABCD) nên SM ⊥ MI.
Tam giác SMI vuông tại M có MH là đường cao
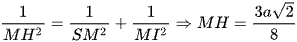
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao