Giải bài tập Bài 6.22 trang 27 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 6.22 trang 27 Toán 10 Tập 2. Bài 18: Phương trình quy về phương trình bậc hai. Toán 10 - Kết nối tri thức
Đề bài:
Bài 6.22 trang 27 Toán 10 Tập 2: Cho tứ giác ABCD có AB ⊥ CD; AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21). Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
Đáp án và cách giải chi tiết:
Đặt AH = x, x > 0.
Xét tam giác AHD vuông tại H, theo định lí Pythagore ta có:
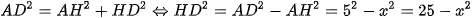
Suy ra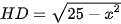 
Ta có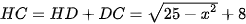 
HB = AH + AB = x + 2
Xét tam giác HBC vuông tại H, theo định lí Pythagore ta có:
BC2 = HB2 + HC2
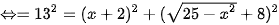
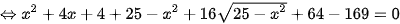
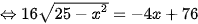
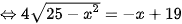
Để tính x, ta cần giải phương trình: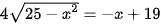 
(1)
Bình phương hai vế của phương trình (1) ta được:
16.(25 – x2) = x2 – 38x + 361
⇔ 17x2 – 38x – 39 = 0
⇔ x = 3 hoặc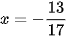 
Thay lần lượt các giá trị trên vào phương trình (1), ta thấy hai giá trị x = 3 và 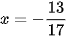đều thỏa mãn.
Vì điều kiện của x là x > 0 nên ta chọn x = 3.
Do đó ta tính được AH = 3.
Suy ra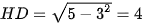 
HC = 4 + 8 = 12
HB = 3 + 2 = 5
Diện tích tam giác HAD là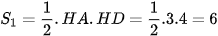 
Diện tích tam giác HBC là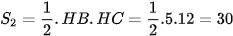
Vậy diện tích tứ giác ABCD là S = S2 – S1 = 30 – 6 = 24.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao