Giải bài tập Bài 6.20 trang 27 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 6.20 trang 27 Toán 10 Tập 2. Bài 18: Phương trình quy về phương trình bậc hai. Toán 10 - Kết nối tri thức
Đề bài:
Bài 6.20 trang 27 Toán 10 Tập 2: Giải các phương trình sau:
a)
;
b)
;
c)
;
d)
.
Đáp án và cách giải chi tiết:
a)
Bình phương hai vế của phương trình ta được:
3x2– 4x – 1 = 2x2 – 4x + 3
⇔ x2 – 4 = 0
⇔ x2 = 4
⇔ x = 2 hoặc x = – 2.
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả hai giá trị x = 2 và x = – 2 thỏa mãn.
Vậy tập nghiệm của phương trình là S = {– 2; 2}.
b)
Bình phương hai vế của phương trình ta được:
x2 + 2x – 3 = – 2x2 + 5
⇔ 3x2 + 2x – 8 = 0
⇔ x = – 2 hoặc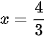
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy chỉ có giá trị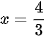 
thỏa mãn.
Vậy nghiệm của phương trình là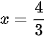
c)
Bình phương hai vế của phương trình ta được:
2x2 + 3x – 3 = – x2 – x + 1
⇔ 3x2 + 4x – 4 = 0
⇔ x = – 2 hoặc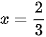 
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả hai giá trị đều không thỏa mãn.
Vậy phương trình vô nghiệm.
d)
Bình phương hai vế của phương trình ta được:
– x2 + 5x – 4 = – 2x2 + 4x + 2
⇔ x2 + x – 6 = 0
⇔ x = – 3 hoặc x = 2.
Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x = 2 thỏa mãn.
Vậy nghiệm của phương trình là x = 2.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao