Giải bài tập Bài 4.19 trang 26 Toán 12 Tập 2 | SGK Toán 12 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 4.19 trang 26 Toán 12 Tập 2. Bài 13. Ứng dụng hình học của tích phân.. SGK Toán 12 - Kết nối tri thức
Đề bài:
Bài 4.19 trang 26 Toán 12 Tập 2: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và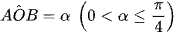 
. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).
a) Tính thể tích V của β theo a và α.
b) Tìm α sao cho thể tích V lớn nhất
Đáp án và cách giải chi tiết:
a) Xét tam giác OAB vuông tại A, có AB = OA.tanα = a.tanα.
Khi quay miền tam giác OAB xung quanh trục Ox ta được khối nón có bán kính đáy r = AB = a.tanα và chiều cao h = OA = a.
Do đó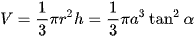 
b) Có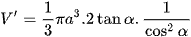 
Vì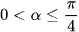 
=> 0 < tanα ≤ 1 nên V' > 0. Do đó V là hàm số đồng biến trên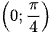 
Do đó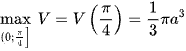 
Vậy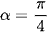 
thì thể tích khối nón là lớn nhất.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao