Giải bài tập Bài 3 trang 56 Toán 11 Tập 2 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 56 Toán 11 Tập 2. Bài 1: Hai đường thẳng vuông góc. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC = a,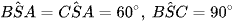 
. Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥ SA và IJ ⊥ BC.
Đáp án và cách giải chi tiết:
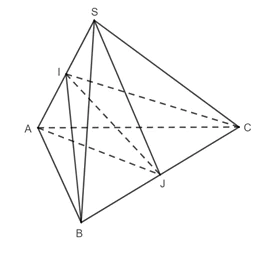
Xét tam giác SAB có:
SA = SB = a
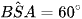
⇒ Tam giác SAB đều.
Mà I là trung điểm của SA ⇒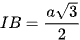 
Xét tam giác SAC có:
SA = SC = a
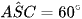
⇒ Tam giác SAC đều.
Mà I là trung điểm của SA ⇒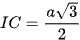 
Ta có BSC là tam giác vuông cân tại S.
⇒ 
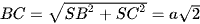
Xét tam giác ABC:
AB = AC = a
AB2 + AC2 = a2 + a2 = 2a2
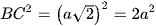
⇒ AB2 + AC2 = BC2
⇒ Tam giác ABC vuông cân tại A.
Mà J là trung điểm đoạn BC ⇒ AJ ⊥ BC
⇒ 
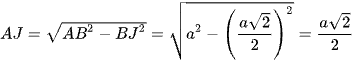
Xét tam giác SBC vuông cân tại S:
Mà J là trung điểm đoạn BC ⇒ SJ ⊥ BC
⇒ 
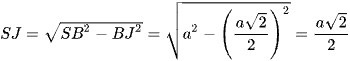
Xét tam giác JSA:
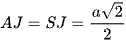
⇒ Tam giác JSA cân tại J.
Mà I là trung điểm của SA ⇒ IJ là đường trung tuyến của tam giác JSA.
hay IJ ⊥SA.
Xét tam giác IBC:
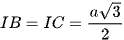
⇒ Tam giác IBC cân tại I.
Mà J là trung điểm của BC ⇒ IJ là đường trung tuyến của tam giác IBC.
hay IJ ⊥BC.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao