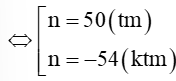Giải bài tập Bài 2.11 trang 51 Toán 11 Tập 1 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 2.11 trang 51 Toán 11 Tập 1. Bài 6: Cấp số cộng. Toán 11 - Kết nối tri thức
Đề bài:
Một cấp số cộng có số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2700?
Đáp án và cách giải chi tiết:
Cấp số cộng có u1 = 5 và d = 2. Giả sử tổng của n số hạng đầu bằng 2700. Khi đó ta có:
.
Do đó,
⇔ n(10 + 2n – 2) = 5 400
⇔ n(2n + 8) – 5 400 = 0
⇔ 2n2 + 8n – 5 400 = 0
Vậy tổng của 50 số hạng đầu của cấp số cộng đã cho bằng 2700.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Loading...