Giải bài tập Bài 1.8 trang 9 SBT Toán 12 Tập | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.8 trang 9 SBT Toán 12 Tập . Bài 1. Tính đơn điệu và cực trị của hàm số.. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.
a) Tính hàm lợi nhuận trung bình
b) Tìm lợi nhuận trung bình khi mức sản xuất x lần lượt là 100, 500 và 1 000 đơn vị sản phẩm.
c) Xét tính đơn điệu của hàm lợi nhuận trung bình trên khoảng (0; +∞) và tính giới hạn của hàm số này khi x → +∞. Giải thích ý nghĩa thực tiễn của kết quả nhận được.
Đáp án và cách giải chi tiết:
a) Ta có:
(triệu đồng).
Tập xác định của hàm lợi nhuận trung bình là: (0; +∞).
b) Với x = 100 thì (triệu đồng).
Với x = 500 thì (triệu đồng).
Với x = 1 000 thì (triệu đồng).
c) Ta có:
với mọi x ∈ (0; +∞).
Vậy hàm lợi nhuận trung bình đồng biến trên khoảng (0; +∞).
Mặt khác,
Ta có bảng biến thiên như sau:
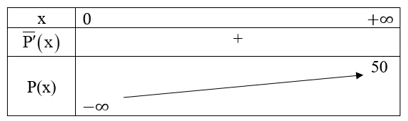
Như vậy, mặc dù lợi nhuận trung bình luôn tăng khi mức sản xuất tăng nhưng không vượt quá 50 triệu đồng.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao