Giải bài tập Vận dụng 4 trang 71 Toán 8 Tập 1 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng 4 trang 71 Toán 8 Tập 1. Bài 3. Hình thang – Hình thang cân. Toán 8 - Chân trời sáng tạo
Đề bài:
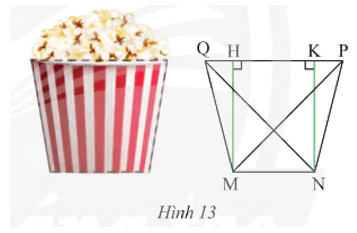
Vận dụng 4 trang 71 Toán 8 Tập 1: Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo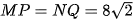 
cm. Tính độ dài đường cao và cạnh bên của hình thang.
Đáp án và cách giải chi tiết:
• MNPQ là hình thang cân nên MN // QP; MQ = NP; 
(tính chất hình thang cân).
• Ta có: MN // QP (chứng minh trên) và NK ⊥ QP (giả thiết)
Suy ra NK ⊥ MN hay 
.
Xét DMHK và DKNM có:
;
MK là cạnh huyền chung;
(hai góc so le trong của QP // MN).
Do đó DMHK = DKNM (cạnh huyền – góc nhọn)
Suy ra HK = NM = 6 cm (hai cạnh tương ứng).
• Xét DMHQ và DNKP có:
;
MQ = NP (chứng minh trên);
(chứng minh trên).
Do đó DMHQ = DNKP (cạnh huyền – góc nhọn).
Suy ra QH = PK (hai cạnh tương ứng).
Mà QH + HK + PK = QP
Hay 2QH = QP – HK
Khi đó 
Nên HP = HK + KP = 6 + 2 = 8 (cm).
• Áp dụng định lí Pythagore vào DMHP vuông tại H, ta có:
MP2 = MH2 + HP2
Suy ra 
Do đó MH = 8 cm.
Áp dụng định lí Pythagore vào DMHQ vuông tại H, ta có:
MQ2 = MH2 + HQ2 = 82 + 22 = 64 + 4 = 68
Suy ra 
(cm).
Vậy hình thang cân MNPQ có độ dài đường cao là MH = NK = 8 cm; độ dài cạnh bên là 
cm.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao