Giải bài tập Khám phá 2 trang 69 Toán 8 Tập 1 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 2 trang 69 Toán 8 Tập 1. Bài 3. Hình thang – Hình thang cân. Toán 8 - Chân trời sáng tạo
Đề bài:
Khám phá 2 trang 69 Toán 8 Tập 1:
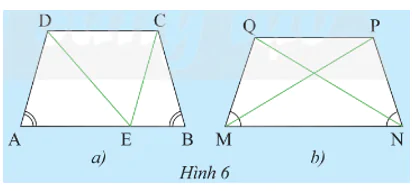
a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a).
i) Tam giác CEB là tam giác gì? Vì sao?
ii) So sánh AD và BC.
b) Cho hình thang cân MNPQ có hai đáy là MN và PQ (Hỉnh 6b). So sánh MP và NQ. Giải thích.
Đáp án và cách giải chi tiết:
a)
i) Xét hình thang cân ABCD (AB // DC) có 
Vì CE // AD nên 
(đồng vị).
Do đó 
Xét DCEB có nên là tam giác cân tại C.
ii) Do DCEB cân tại C (câu i) nên CE = CB (1)
Xét DADE và DCED có:
(hai góc so le trong của AD // CE);
DE là cạnh chung;
(hai góc so le trong của DC // AB).
Do đó DADE = DCED (g.c.g).
Suy ra AD = CE (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có AD = BC.
b) Áp dụng kết quả của phần ii) câu a) ở trên cho hình thang cân MNPQ ta có MQ = NP.
Xét hình thang cân MNPQ (MN // QP) có 
Xét DMNQ và DNMP có:
MQ = NP (chứng minh trên);
(chứng minh trên);
MN là cạnh chung.
Do đó DMNQ = DNMP (c.g.c)
Suy ra NQ = MP (hai cạnh tương ứng).
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao