Giải bài tập Luyện tập 4 trang 83 Toán 12 Tập 2 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 4 trang 83 Toán 12 Tập 2. Bài 3. Phương trình mặt cầu.. SGK Toán 12 - Cánh diều
Đề bài:
Chứng minh rằng phương trình x2 + y2 + z2 – 6x – 2y – 4z – 11 = 0 là phương trình của một mặt cầu. Tìm tâm I và bán kính R của mặt cầu đó.
Đáp án và cách giải chi tiết:
Cách 1:
Ta có x2 + y2 + z2 – 6x – 2y – 4z – 11 = 0
⇔ x2 – 2.3.x + 9 + y2 – 2.1.y + 1 + z2 – 2.2.z + 4 = 9 + 1 + 4 + 11
⇔ (x – 3)2 + (y – 1)2 + (z – 2)2 = 25.
Vậy phương trình đã cho là phương trình của một mặt cầu có tâm I(3; 1; 2) và bán kính R = 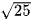 = 5.
= 5.
Cách 2:
Ta có x2 + y2 + z2 – 6x – 2y – 4z – 11 = 0
⇔ x2 + y2 + z2 – 2.3.x – 2.1.y – 2.2.z – 11 = 0
Khi đó a2 + b2 + c2 – d = 32 + 12 + 22 – (– 11) = 25 > 0.
Vậy phương trình đã cho là phương trình của một mặt cầu có tâm I(3; 1; 2) và bán kính R = 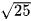 = 5.
= 5.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao