Giải bài tập Bài 23 trang 51 SBT Toán 12 Tập 2 | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 23 trang 51 SBT Toán 12 Tập 2. Bài tập ôn tập cuối năm. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số y = −x3 + 3x2 – 2.
b) Tìm điều kiện của tham số m để phương trình x3 – 3x2 + 5 – m = 0 có ba nghiệm phân biệt.
c) Tìm điểm thuộc đồ thị hàm số mà tiếp tuyến với đồ thị tại điểm có hệ số góc lớn nhất.
Đáp án và cách giải chi tiết:
a) Tập xác định: D = ℝ.
Ta có: y' = −3x2 + 6x
y' = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên sau:
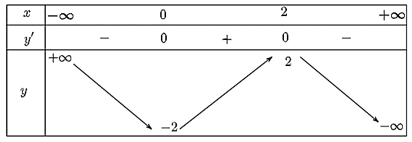
Hàm số đồng biến trên khoảng (0; 2).
Hàm số nghịch biến trên khoảng (−∞; 0) và (2; +∞).
Điểm cực đại và cực tiểu của hàm số lần lượt là (2; 2) và (0; −2).
Đồ thị hàm số nhận điểm uốn I(1; 0) làm tâm đối xứng.

b) Ta có: x3 – 3x2 + 5 – m = 0 ⇔ −x3 + 3x2 – 2 = 3 – m.
Vậy phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y = 3 – m cắt đồ thị y = −x3 + 3x2 – 2 tại ba điểm phân biệt.
Điều này tương đương với −2 < 3 – m < 2 ⇔ 1 < m < 5.
c) Ta có: y' = −3x2 + 6x = (−3x2 + 6x – 3) + 3 = −3(x – 1)2 + 3 ≤ 3, ∀x ∈ ℝ.
Vậy tiếp tuyến có hệ số góc lớn nhất bằng 3 tại x = 1.
Phương trình tiếp tuyến này là y = y'(1)(x – 1) + y(1)
⇔ y = 3(x – 1) + 0
⇔ y = 3x – 3.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao