Giải bài tập Bài 12 trang 88 Toán 12 Tập 2 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 12 trang 88 Toán 12 Tập 2. Bài tập cuối chương 5. SGK Toán 12 - Cánh diều
Đề bài:
Bài 12 trang 88 Toán 12 Tập 2: Trong không gian với hệ trục toạ độ Oxyz, cho hình lập phương OBCD.O'B'C'D' có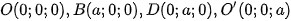 
với a > 0.
a) Chứng minh rằng đường chéo O'C vuông góc với mặt phẳng (OB'D').
b) Chứng minh rằng giao điểm của đường chéo O'C và mặt phẳng (OB'D') là trọng tâm của tam giác OB'D'.
c) Tính khoảng cách từ điểm B' đến mặt phẳng (C'BD).
d) Tính côsin góc giữa hai mặt phẳng (CO'D) và (C'BD).
Đáp án và cách giải chi tiết:
Gọi tọa độ điểm C là 
. Ta có 
Vì OBCD.O'B'C'D' là hình lập phương nên OBCD là hình vuông, do đó ta có
Suy ra 
.
Gọi tọa độ điểm B' là 
. Ta có 
.
Ta có 
. Suy ra 
.
Gọi tọa độ điểm D' là 
. Khi đó 
.
Ta có 
. Suy ra 
.
a) Ta có 
Xét vectơ 
Khi đó 
là một vectơ pháp tuyến của mặt phẳng (OB'D').
Lại có 
. Ta có 
, suy ra hai vectơ 
cùng phương.
Do đó, 
cũng là một vectơ pháp tuyến của mặt phẳng (OB'D').
Vậy đường chéo O'C vuông góc với mặt phẳng (OB'D').
b) Phương trình tổng quát của mặt phẳng (OB'D') đi qua điểm O và nhận làm vectơ pháp tuyến là: 
(do a>0).
Phương trình tham số của đường thẳng O'C đi qua đi qua điểm 
và nhận 
làm vectơ chỉ phương là: 
(t là tham số).
Gọi G là giao điểm của đường chéo O'C và mặt phẳng (OB'D').
Vì 
nên gọi tọa độ điểm G là 
.
Mà 
nên ta có 
, suy ra 
. Do đó 
.
Tọa độ trọng tâm G' của tam giác OB'D': 
.
Suy ra 
. Do đó, 
.
Vậy giao điểm của đường chéo O'C và mặt phẳng (OB'D') là trọng tâm của tam giác OB'D'.
c) Gọi tọa độ điểm C' là 
. Khi đó 
.
Ta có 
. Suy ra 
.
Ta có 
.
Xét vectơ 
.
Khi đó, 
là một vectơ pháp tuyến của mặt phẳng (C'BD).
Phương trình tổng quát của mặt phẳng (C'BD) là: 
.
Khoảng cách từ điểm B' đến mặt phẳng (C'BD) là:
(do a > 0).
d) Ta có 
.
Xét vectơ 
.
Khi đó,
là một vectơ pháp tuyến của mặt phẳng (CO'D).
Ta có 
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao