Giải bài tập Vận dụng 1 trang 77 Toán 9 Tập 2 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng 1 trang 77 Toán 9 Tập 2. Bài 3. Đa giác đều và phép quay. Toán 9 - Chân trời sáng tạo
Đề bài:
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?
Đáp án và cách giải chi tiết:
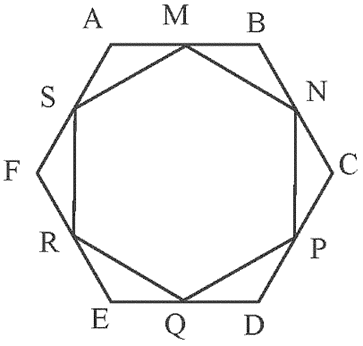
Do ABCDEF là lục giác đều nên
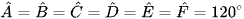
• AB = BC = CD = DE = EF = FA.
Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.
Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.
Xét ΔSAM và ΔMBN có:
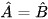(chứng minh trên);
AM = BN (chứng minh trên);
SA = MB (chứng minh trên).
Do đó ΔSAM = ΔMBN (c.g.c).
Suy ra SM = MN (hai cạnh tương ứng).
Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM. (1)
Vì AS = AM (chứng minh trên) suy ra ΔASM cân tại A.
Suy ra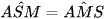 
(tính chất tam giác cân).
Do đó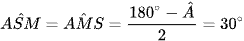 
(tổng 3 góc trong của tam giác).
Tương tự ta thu được:
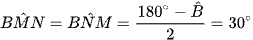
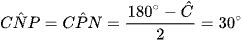
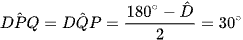
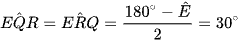
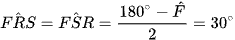
Ta có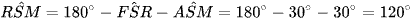 
Tương tự, ta được: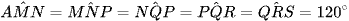 
(2).
Từ (1) và (2), suy ra MNPQRS là đa giác đều.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao