Giải bài tập Khám phá 3 trang 75 Toán 8 Tập 1 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 3 trang 75 Toán 8 Tập 1. Bài 4. Hình bình hành – Hình thoi. Toán 8 - Chân trời sáng tạo
Đề bài:
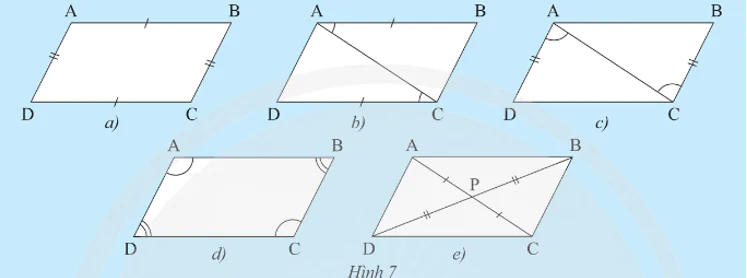
Khám phá 3 trang 75 Toán 8 Tập 1: Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:
Trường hợp 1: AB = CD và AD = BC (Hình 7a).
Trường hợp 2: AB // CD và AB = CD (Hình 7b).
Trường hợp 3: AD // BC và AD = BC (Hình 7c).
Trường hợp 4: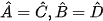 
(Hình 7d).
Trường hợp 5: PA = PC, PB = PD (Hình 7e).
Đáp án và cách giải chi tiết:
• Hình 7a):
Xét DABC và DCDA có:
AB = CD; BC = DA; AC là cạnh chung
Do đó DABC = DCDA (c.c.c)
Suy ra 
và 
(các cặp góc tương ứng).
Vì và hai góc này ở vị trí so le trong nên AB // CD.
Vì và hai góc này ở vị trí so le trong nên AD // BC.
• Hình 7b):
Ta có và hai góc này ở vị trí so le trong nên AB // CD.
Xét DABC và DCDA có:
AC là cạnh chung; ; AB = CD
Do đó DABC = DCDA (c.g.c)
Suy ra (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AD // BC.
• Hình 7c):
Ta có: và hai góc này ở vị trí so le trong nên AD // BC.
Xét DABC và DCDA có:
AC là cạnh chung; ; BC = AD
Do đó DABC = DCDA (c.g.c)
Suy ra (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB // CD.
• Hình 7d):
Xét tứ giác ABCD ta có 
(định lí tổng các góc của một tứ giác)
Mà 
nên ta có 
Suy ra 
và 
Do đó AD // BC và AB // CD.
• Hình 7e):
Xét DPAB và DPCD có:
PA = PC;
(đối đỉnh); PB = PD
Do đó DPAB = DPCD (c.g.c)
Suy ra 
(hai góc tương ứng)
Hay mà hai góc này ở vị trí so le trong nên AB // CD.
Tương tự ta cũng chứng minh được DPAD = DPCB (c.g.c)
Suy ra 
(hai góc tương ứng)
Hay 
, mà hai góc này ở vị trí so le trong nên AD // BC.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao