Giải bài tập Khám phá 2 trang 68 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 2 trang 68 Toán 8 Tập 2. Bài 2. Các trường hợp đồng dạng của hai tam giác.. Toán 8 - Chân trời sáng tạo
Đề bài:
Cho tam giác DEF và ABC có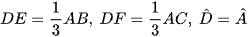 
(Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC (N ∈ AC).
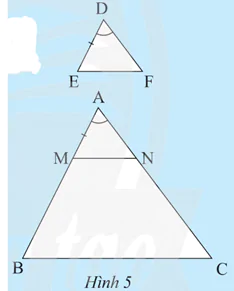
a) So sánh các tỉ số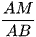 
và 
.
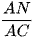b) So sánh AN và DF.
c) Tam giác AMN có đồng dạng với tam giác ABC không?
d) Dự đoán sự đồng dạng của hai tam giác DEF và ABC.
Đáp án và cách giải chi tiết:
a) Tam giác ABC có MN // BC, theo định lí Thalès, ta có: 
.
b) Ta có 
; AM = DF suy ra AN = DF.
c) Tam giác ABC có MN cắt AB, AC lần lượt tại M và N và MN // BC.
Do đó ΔAMN ᔕ ΔABC.
d) Xét ∆DEF và ∆AMN có:
DE = AM (gt)
DF = AN (cmt)
Do đó ΔDEF = ΔAMN (c.g.c)
Dự đoán: ΔDEF ᔕ ΔABC.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao