Giải bài tập Bài 6 trang 71 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 6 trang 71 Toán 8 Tập 2. Bài 2. Các trường hợp đồng dạng của hai tam giác.. Toán 8 - Chân trời sáng tạo
Đề bài:
a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF.
b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABC ᔕ ΔMED.
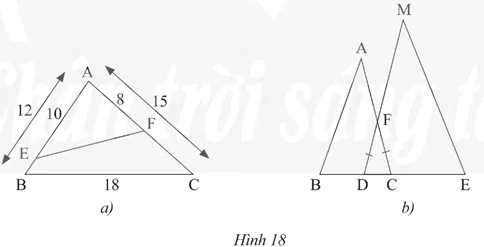
Đáp án và cách giải chi tiết:
a) Xét ΔAFE và ΔABC có:
chung
Do đó ΔAFE ᔕ ΔABC (c.g.c)
Suy ra 
(các cặp cạnh tương ứng).
Khi đó 
suy ra 
.
Vậy EF = 12 cm.
b) Xét ΔABC và ΔMED ta có:
(tam giác FDC cân)
Vậy ΔABC ᔕ ΔMED (c.g.c).
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao