Giải bài tập Bài 7 trang 78 Toán 9 Tập 2 | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 7 trang 78 Toán 9 Tập 2. Bài 2. Tứ giác nội tiếp đường tròn. Toán 9 - Cánh diều
Đề bài:
Bài 7 trang 78 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H (Hình 30).
Chứng minh:
a)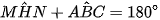 
;
b) 
c)
.
Đáp án và cách giải chi tiết:
a) Xét ∆ABC có hai đường cao AM và CN cắt nhau tại H nên AM ⊥ BC và CN ⊥ AB, do đó 
Xét tứ giác HMBN có:
(tổng các góc của một tứ giác)
Suy ra 
Hay 
b) Vì tứ giác ABCD là tứ giác nội tiếp nên tổng hai góc đối nhau bằng 180°.
Do đó 
Mà 
(câu a) nên 
Lại có 
(đối đỉnh) nên 
c) Xét ∆AHN vuông tại N có 
là góc ngoài của tam giác tại đỉnh H nên 
(tính chất góc ngoài của một tam giác).
Mà 
(câu b) nên 
.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao