Giải bài tập Bài 3 trang 88 Toán 12 Tập 1 | SGK Toán 12 - Cánh diều

Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 88 Toán 12 Tập 1. Bài 1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm.. SGK Toán 12 - Cánh diều

Đề bài:

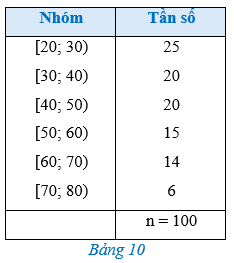
Bài 3 trang 88 Toán 12 Tập 1: Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.

a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.

Đáp án và cách giải chi tiết:

a) Trong mẫu số liệu ghép nhóm ở Bảng 10, ta có: đầu mút trái của nhóm 1 là $a_{1} = 20$ , đầu mút phải của nhóm 6 là $a_{7} = 80$ .

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

$R = a_{7} - a_{1} = 80 - 20 = 60$ .

b) Từ Bảng 10 ta có bảng sau:

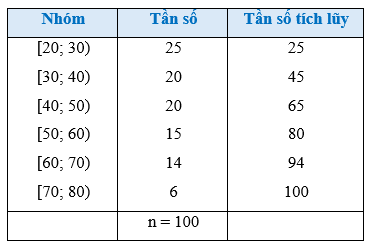
Số phần tử của mẫu là n = 100.

- Ta có: $\frac{n}{4} = \frac{100}{4} = 25$ . Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm 1 là nhóm [20; 30) có s = 20; h = 10; n₁ = 25.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 20 + \frac{25}{25} . 10 = 30$ .

- Ta có: $\frac{3 n}{4} = \frac{3.100}{4} = 75$ mà $65 < 75 < 80$ . Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm [50; 60) có t = 50; l = 10; n₄ = 15 và nhóm 3 là nhóm [40; 50) có $c f_{3} = 65$ .