Giải bài tập Bài 2 trang 97 Toán 9 Tập 1 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 97 Toán 9 Tập 1. Bài 3. Góc ở tâm. Góc nội tiếp. Toán 9 - Chân trời sáng tạo
Đề bài:
Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung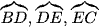 
.
Đáp án và cách giải chi tiết:
Gọi O là trung điểm của BC. Khi đó ta có đường tròn (O) đường kính BC chứa các cung BD, DE, EC.
Vì ∆ABC là tam giác đều nên 
.
Xét ∆OBD có OB = OD (cùng bằng bán kính đường tròn (O) đường kính BC) nên ∆OBD cân tại O.
Lại có 
nên ∆OBD là tam giác đều, suy ra 
. Khi đó 
(1).
Tương tự, ta cũng có ∆OCE là tam giác đều, suy ra 
. Khi đó 
(2).
Ta có BC là đường kính của đường tròn nên 
.
Có 
.
Suy ra 
.
Do đó 
. Khi đó 
(3).
Từ (1), (2) và (3) ta có: 
(=60°).
Do đó các cung BD, DE, EC bằng nhau.
Nguồn: giaitoanhay.com
Tổng số đánh giá:
Xếp hạng: / 5 sao