Giải bài tập Bài 10 trang 85 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo

Hướng dẫn giải chi tiết từng bước bài tập Bài 10 trang 85 Toán 8 Tập 2. Bài tập cuối chương 8.. Toán 8 - Chân trời sáng tạo

Đề bài:

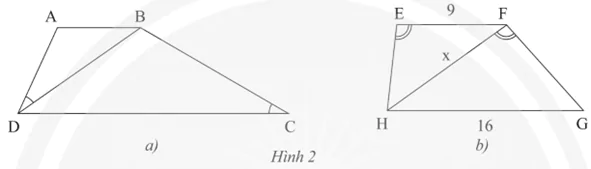
a) Cho hình thang ABCD (AB // CD), biết 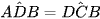 (Hình 2a). Chứng minh rằng BD2 = AB.CD.

b) Cho hình thang EFGH (EF // GH), 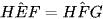, EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF.

Đáp án và cách giải chi tiết:

a) Xét ΔABD và ΔBDC có: 

(gt)

 (AB // CD, hai góc so le trong)

Do đso ΔABD ᔕ ΔBDC (g.g)

Suy ra  (các cạnh tương ứng).

Vậy BD2 = AB.CD (đpcm).

b) Tương tự câu a, ta có:

Xét tam giác EFH và FHG ta có:

Do đó ΔEFH ᔕ ΔFHG (g.g)

Suy ra  (các cạnh tương ứng).

Khi đó HF2 = EF.GH = 9.16 = 144 nên HF = 12 cm.

Nguồn: giaitoanhay.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Giải bài tập Toán 8 - Chân trời sáng tạo

Xem tất cả Bài 1. Đơn thức và đa thức nhiều biến Bài 2. Các phép toán với đa thức nhiều biến Bài 3. Hằng đẳng thức đáng nhớ Bài 4. Phân tích đa thức thành nhân tử Bài 5. Phân thức đại số Bài 6. Cộng, trừ phân thức Bài 7. Nhân, chia phân thức Bài tập cuối chương 1
Xem tất cả Bài 1. Hình chóp tam giác đều – Hình chóp tứ giác đều Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều Bài tập cuối chương 2 Các hình khối trong thực tiễn
Xem tất cả Bài 1. Định lí Pythagore Bài 2. Tứ giác Bài 3. Hình thang – Hình thang cân Bài 4. Hình bình hành – Hình thoi Bài 5. Hình chữ nhật – Hình vuông Bài tập cuối chương 3 Định lý Pythagore. Các loại tứ giác thường gặp
Xem tất cả Bài 1. Thu thập và phân loại dữ liệu Bài 2. Lựa chọn dạng biểu đồ để biểu diễn dữ liệu Bài 3. Phân tích dữ liệu Bài tập cuối chương 4 Một số yếu tố thống kê
Xem tất cả Hoạt động 1. Dùng vật liệu tái chế gấp hộp quà tặng. Hoạt động 2. Làm tranh treo tường minh hoạ các loại hình tứ giác đặc biệt. Hoạt động 3. Thiết lập kế hoạch cho một mục tiêu tiết kiệm.
Xem tất cả Bài 1. Khái niệm hàm số Bài 2. Toạ độ của một điểm và đồ thị của hàm số Bài 3. Hàm số bậc nhất y = ax + b (a khác 0) Bài 4. Hệ số góc của đường thẳng Bài tập cuối chương 5 Hàm số và đồ thị
Xem tất cả Bài 1. Phương trình bậc nhất một ẩn. Bài 2. Giải bài toán bằng cách lập phương trình bậc nhất. Bài tập cuối chương 6.
Xem tất cả Bài 1. Định lí Thalès trong tam giác. Bài 2. Đường trung bình của tam giác. Bài 3. Tính chất đường phân giác của tam giác. Bài tập cuối chương 7.
Xem tất cả Bài 1. Hai tam giác đồng dạng. Bài 2. Các trường hợp đồng dạng của hai tam giác. Bài 3. Các trường hợp đồng dạng của hai tam giác vuông. Bài 4. Hai hình đồng dạng. Bài tập cuối chương 8.
Xem tất cả Bài 1. Mô tả xác suất bằng tỉ số. Bài 2. Xác suất lí thuyết và xác suất thực nghiệm. Bài tập cuối chương 9.
Xem tất cả Hoạt động 4. Vẽ đồ thị hàm số bậc nhất y = ax + b bằng phần mềm GeoGebra. Hoạt động 5. Dùng phương trình bậc nhất để tính nồng độ phần trăm của dung dịch. Thực hành pha chế dung dịch nước muối sinh lí. Hoạt động 6. Ứng dụng định lí Thalès để ước lượng tỉ lệ giữa chiều ngang và chiều dọc của một vật.